피보나치 수
피보나치 수의 첫 번째 항과 두 번째 항은 1입니다.
그 이후의 각 용어는 이전 두 용어의 합계입니다. 시리즈
처음 6항은 각각 1, 1, 2, 3, 5, 8입니다.
간단하게 하기 위해 0번째 항은 때때로 0으로 설정됩니다.
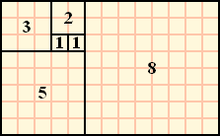
콘텐츠 소스 – 위키백과 –
구현하는 경우
자바
public static Long fibo(Long n) {
if(n == 1 || n == 2) return 1L;
return fibo(n-1) + fibo(n-2);
}
파이썬
def fibo(n):
if n in (1, 2):
return 1
return fibo(n-1) + fibo(n-2)
실행문의 길이는 2-3줄에 불과합니다.
그건 매우 쉬워요. 하지만…
fibo(1) : 1
fibo(2) : 1
fibo(3) : fibo(2) + fibo(1)
= 1 + 1 = 2
fibo(4) : fibo(3) + fibo(2)
= fibo(2) + fibo(1) + fibo(2)
= 1 + 1 + 1 = 3
fibo(5) : fibo(4) + fibo(3)
= fibo(3) + fibo(2) + fibo(2) + fibo(1)
= fibo(2) + fibo(1) + fibo(2) + fibo(2) + fibo(1)
= 1 + 1 + 1 + 1 + 1
= 5
fibo(6) : fibo(5) + fibo(4)
= fibo(4) + fibo(3) + fibo(3) + fibo(2)
= fibo(3) + fibo(2) + fibo(2) + fibo(1) + fibo(2) + fibo(1) + fibo(2)
= fibo(2) + fibo(1) + fibo(2) + fibo(2) + fibo(1) + fibo(2) + fibo(1) + fibo(2)
= 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1
= 8
.
.
.
나는 그것을 직접 시도
적은 수라도 기하급수적으로 늘어남
계산 횟수가 증가합니다.
컴퓨터가 이것을 할 때
30, 40, 50… 100 이상
나중에 컴퓨터를 켜고 밥을 먹어도
달릴 것이다

파이보(100) = 354224848179261915075
fib(5) 작업
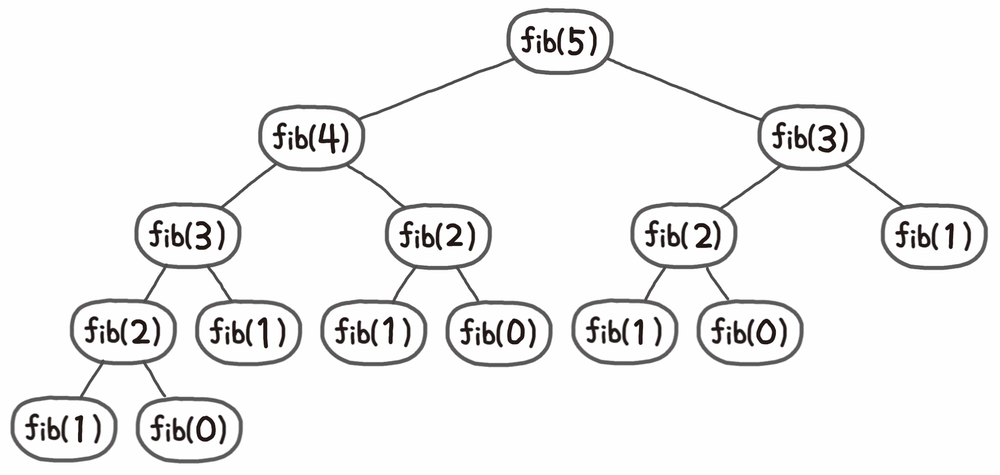
사진을 봐
섬유질을 얻으십시오 (5)
fib(3)이 두 번 발견되었습니다.
시퀀스가 클수록 중복 수가 더 많습니다.
계산을 많이 하세요.
그러면 당연히 컴퓨팅 속도가 느려질 수밖에 없습니다.
암기하다사용
계산 결과 저장
이전 작업 결과를 바로 불러올 수 있기 때문에
시간이 지남에 따라 크게 감소합니다.
동적 프로그래밍의 핵심이라고 한다
메모이제이션을 사용하여 자바 코드를 작성했습니다.
Java에서 Map으로 구현되었습니다.
import java.util.HashMap;
import java.util.Map;
public class Main {
static Map<Long, Long> memo = new HashMap<>();
public static void main(String() args) {
System.out.println(getFiboNum(100L));
}
public static long getFiboNum(Long n) {
memo.put(1L, 1L);
memo.put(2L, 1L);
if(memo.containsKey(n)) return memo.get(n);
memo.put(n, getFiboNum(n-1) + getFiboNum(n-2) );
return memo.get(n);
}
}
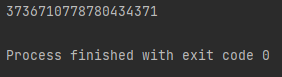
또한 메모이제이션을 사용하여 Python 코드를 작성했습니다.
memo = {1: 1, 2: 1}
def fibo(n) :
if n in memo:
return memo(n)
memo(n) = fibo(n-1) + fibo(n-2)
return memo(n)
print(fibo(100))
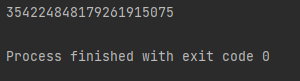
파이썬과 자바에서
피보나치 수열의 구현.
메모를 사용
시간 절약 효과가 엄청날 것입니다
그것을 경험했다

